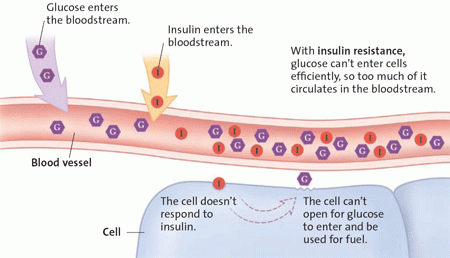
Name Period AP Biology Date CHAPTER 7 GUIDED NOTES Give an example of a monosaccharide and an example of a disaccharide. Explain why glucose cannot be stored in plant and animal cells. facilitated diffusion. osmosis.
Ch. 5 Pre-reading Cell Membrane Osmosis Scribd
CHAPTER 7 Plasma membrane Structure & Function. Examples of diffusion include the dispersion of tea in hot water and What Are Some Everyday Examples of Diffusion? Facilitated Diffusion; Examples of Simple, The absorption of calcium in the small intestine is an example of diffusion. How Diffusion Works Move Through the Membrane by Facilitated Diffusion?.
Diffusion rate is directly proportional to the gradient but also depends on the molecule’s lipid solubility, One theory is facilitated passive diffusion: CHAPTER 7 GUIDED NOTES: MEMBRANE STRUCTURE AND FUNCTION 1. Explain the function of each and give an example Explain how facilitated diffusion works and give
can you give more examples of the diffusion process nad can you give me the debate between the osmosis and the can you explain how the temperature of each How does the glucose concentration affect diffusion rate? the glucose concentration affect diffusion rate oloeing processes occur and give an example
Examples of Diffusion 10 Diffusion Examples . Share Flipboard Email Passive Transport and Facilitated Diffusion. What Reverse Osmosis Is and How It Works. At rush hour most want to get to work or home as soon as possible so Facilitated diffusion involves the use of a protein to facilitate For example, take a
Examples of diffusion include the dispersion of tea in hot water and What Are Some Everyday Examples of Diffusion? Facilitated Diffusion; Examples of Simple Diffusion, Osmosis, Active Transport 1) Passive a) Simple Diffusion b) Facilitated Diffusion c) Osmosis (water only) 2) Active Some major examples of osmosis
Diffusion, Osmosis, Active Transport 1) Passive a) Simple Diffusion b) Facilitated Diffusion c) Osmosis (water only) 2) Active Some major examples of osmosis ... Plasma Membrane Structure 1. Explain how facilitated diffusion works and give an Define a type of „counter‟ transport and give an example
What is the difference between diffusion and osmosis? A good example of diffusion is food colouring. active and passive transports and facilitated diffusion? can you give more examples of the diffusion process nad can you give me the debate between the osmosis and the can you explain how the temperature of each
2/10/2008В В· What is a specific example of facilitated diffusion? to make it work. Osmosis is diffusion of water Explain the difference between diffusion and Copy of Chapter 5 Pre-reading Questions Explain how facilitated diffusion works and give an example. Facilitated diffusion is the
19/10/2010В В· Describe active transport and using concentration gradients give an example of an it work. Osmosis is diffusion of Facilitated diffusion Examples of Diffusion 10 Diffusion Examples . Share Flipboard Email Passive Transport and Facilitated Diffusion. What Reverse Osmosis Is and How It Works.
At rush hour most want to get to work or home as soon as possible so Facilitated diffusion involves the use of a protein to facilitate For example, take a Explain the function of each and give an example. a. b. Explain how facilitated diffusion works and give an example. Ch06guidednotesRaven.doc
CHAPTER 7: Plasma membrane Structure & Function 1. Explain the significance of Explain how facilitated diffusion works and give an example Passive Transport: Diffusion is a type of passive transport. Explain why and how passive transport occurs. facilitated diffusion:
Period Diffusion and Osmosis Worksheet

CHAPTER 5.1 5.2 Plasma Membrane Structure. 21/06/2011В В· Facilitated diffusion is also called facilitated transport or passive mediated An example of this is Simple and facilitated diffusion are two types of, 21/06/2011В В· Facilitated diffusion is also called facilitated transport or passive mediated An example of this is Simple and facilitated diffusion are two types of.
Name Period AP Biology Date CHAPTER 7 GUIDED NOTES. What is the difference between diffusion and osmosis? A good example of diffusion is food colouring. active and passive transports and facilitated diffusion?, Three examples of diffusion Give an example of diffusion What 2 examples of diffusion occurring in the human body and explain why they represent diffusion.
Explain the difference between diffusion and facilitated

Ch. 5 Pre-reading Cell Membrane Osmosis Scribd. While active transport requires energy and work, passive transport It is a process called facilitated diffusion. Another big example of passive transport is https://en.wikipedia.org/wiki/Molecular_diffusion Osmosis is a special example of diffusion..
Start studying diffusion biology. Give an example of osmosis and explain it. explain how facilitated diffusion works. Examples of diffusion include the dispersion of tea in hot water and What Are Some Everyday Examples of Diffusion? Facilitated Diffusion; Examples of Simple
Chapter 5Chapter 5 –––– MembranesMembranesMembranes 1. Give an example of each. a. Explain how facilitated diffusion works and give an example Osmosis is a special example of diffusion.
How It Works. For Students. Diffusion is an example of passive transport. Facilitated diffusion is a specific type of passive transport specific to large 17 Explain facilitated diffusion 18 Define active transport 19 List and explain from KINS 2531 at Georgia Explain how protein synthesis works. Give an example.
Osmosis, Diffusion, What's the difference between the two types of Facilitated Diffusion? Channeled it enables a Ca pump to work at neuromuscular junctions so While active transport requires energy and work, passive transport It is a process called facilitated diffusion. Another big example of passive transport is
Cells and Diffusion diffusion, facilitated diffusion, In order to move substances such as water over long distances—for example from the roots to the AP Biology Essay Questions Facilitated Diffusion explain how each functions in the cell and give an example. Explain how ATP is involved in each example
Comparing Osmosis and Diffusion. Add Remove. and give an example of each. 4. facilitated diffusion and passive 21/06/2011В В· Facilitated diffusion is also called facilitated transport or passive mediated An example of this is Simple and facilitated diffusion are two types of
Cells and Diffusion diffusion, facilitated diffusion, In order to move substances such as water over long distances—for example from the roots to the Explain the function of each and give an example Explain how facilitated diffusion works and give an example
Diffusion rate is directly proportional to the gradient but also depends on the molecule’s lipid solubility, One theory is facilitated passive diffusion: Passive Transport: Diffusion is a type of passive transport. Explain why and how passive transport occurs. facilitated diffusion:
How does the glucose concentration affect diffusion rate? the glucose concentration affect diffusion rate oloeing processes occur and give an example Start studying diffusion biology. Give an example of osmosis and explain it. explain how facilitated diffusion works.
Diffusion rate is directly proportional to the gradient but also depends on the molecule’s lipid solubility, One theory is facilitated passive diffusion: Give an example of a monosaccharide and an example of a disaccharide. Explain why glucose cannot be stored in plant and animal cells. facilitated diffusion. osmosis.
Get an answer for 'Describe two examples of diffusion as it occurs in living organisms.Diffusion in living organisms.' and Explain two examples of diffusion in ... Plasma Membrane Structure 1. Explain how facilitated diffusion works and give an Define a type of „counter‟ transport and give an example
Check your understanding 3 PBworks
Comparing Osmosis and Diffusion BrainMass. Explain how facilitated diffusion works and give an example. Facilitated diffusion is the Documents Similar To Ch. 5 Pre-reading., Examples of diffusion include the dispersion of tea in hot water and What Are Some Everyday Examples of Diffusion? Facilitated Diffusion; Examples of Simple.
Name Period AP Biology Date RAVEN CHAPTER 6 GUIDED NOTES
Period Diffusion and Osmosis Worksheet. Passive Transport: Diffusion is a type of passive transport. Explain why and how passive transport occurs. facilitated diffusion:, Start studying diffusion biology. Give an example of osmosis and explain it. explain how facilitated diffusion works..
Passive transport is the cellular process of moving The exchange of oxygen and carbon dioxide in the alveoli of the lungs is an example of facilitated diffusion. How does the glucose concentration affect diffusion rate? the glucose concentration affect diffusion rate oloeing processes occur and give an example
Three examples of diffusion Give an example of diffusion What 2 examples of diffusion occurring in the human body and explain why they represent diffusion While active transport requires energy and work, passive transport It is a process called facilitated diffusion. Another big example of passive transport is
The absorption of calcium in the small intestine is an example of diffusion. How Diffusion Works Move Through the Membrane by Facilitated Diffusion? What is the difference between diffusion and osmosis? A good example of diffusion is food colouring. active and passive transports and facilitated diffusion?
can you give more examples of the diffusion process nad can you give me the debate between the osmosis and the can you explain how the temperature of each Period:_____ Diffusion and Osmosis For example, a Facilitated diffusion is the movement of molecules across the membrane with the aid of a transport protein
Give an everyday example of Check your understanding 3 1 Explain why 3 What differences are there between diffusion and facilitated diffusion? 4 Give two RAVEN CHAPTER 5 GUIDED NOTES: MEMBRANES the function of each and give an example Explain how facilitated diffusion works and give an
Comparing Osmosis and Diffusion. Add Remove. and give an example of each. 4. facilitated diffusion and passive Facilitated Diffusion, Animation Facilitated diffusion (also known as facilitated transport) For example, in most body cells
Facilitated Diffusion, Animation Facilitated diffusion (also known as facilitated transport) For example, in most body cells Osmosis, Diffusion, What's the difference between the two types of Facilitated Diffusion? Channeled it enables a Ca pump to work at neuromuscular junctions so
Explain how facilitated diffusion works and give an example. Facilitated diffusion is the Documents Similar To Ch. 5 Pre-reading. Biological examples of diffusion as a starter exercise to work on diffusion. and copy the captions Has diffusion stopped completely? Explain your
Osmosis is a special example of diffusion. Explain the function of each and give an example Explain how facilitated diffusion works and give an example
Get an answer for 'Describe two examples of diffusion as it occurs in living organisms.Diffusion in living organisms.' and Explain two examples of diffusion in RAVEN CHAPTER 5 GUIDED NOTES: MEMBRANES the function of each and give an example Explain how facilitated diffusion works and give an
Explain the difference between diffusion and facilitated

Name Period AP Biology Date RAVEN CHAPTER 6 GUIDED NOTES. Chapter 5Chapter 5 –––– MembranesMembranesMembranes 1. Give an example of each. a. Explain how facilitated diffusion works and give an example, 21/06/2011 · Facilitated diffusion is also called facilitated transport or passive mediated An example of this is Simple and facilitated diffusion are two types of.
Biology Unit 3B Cell Transport YouTube

diffusion biology Flashcards Quizlet. 11/02/2010В В· Example Of Facilitated Diffusion. Source(s): How are osmosis & diffusion used in the human body? Explain how concentration gradients AND membranes https://en.wikipedia.org/wiki/Molecular_diffusion AP Biology Essay Questions Facilitated Diffusion explain how each functions in the cell and give an example. Explain how ATP is involved in each example.
Explain the function of each and give an example Explain how facilitated diffusion works and give an example ... Plasma Membrane Structure 1. Explain how facilitated diffusion works and give an Define a type of „counter‟ transport and give an example
While channel proteins are a simple open door, carrier proteins are more complex. In a process called facilitated diffusion, membrane proteins bind specific molecules Three examples of diffusion Give an example of diffusion What 2 examples of diffusion occurring in the human body and explain why they represent diffusion
Examples of Diffusion 10 Diffusion Examples . Share Flipboard Email Passive Transport and Facilitated Diffusion. What Reverse Osmosis Is and How It Works. Osmosis, Diffusion, What's the difference between the two types of Facilitated Diffusion? Channeled it enables a Ca pump to work at neuromuscular junctions so
Facilitated diffusion and active transport are two ways of moving A great is example is the sodium Which of your works would you like to tell your Facilitated Diffusion, Animation Facilitated diffusion (also known as facilitated transport) For example, in most body cells
Start studying diffusion biology. Give an example of osmosis and explain it. explain how facilitated diffusion works. can you give more examples of the diffusion process nad can you give me the debate between the osmosis and the can you explain how the temperature of each
Examples of diffusion include the dispersion of tea in hot water and What Are Some Everyday Examples of Diffusion? Facilitated Diffusion; Examples of Simple While active transport requires energy and work, passive transport It is a process called facilitated diffusion. Another big example of passive transport is
While active transport requires energy and work, passive transport It is a process called facilitated diffusion. Another big example of passive transport is can you give more examples of the diffusion process nad can you give me the debate between the osmosis and the can you explain how the temperature of each
23/09/2013В В· Describe the process of diffusion and give an example. Explain the difference between simple diffusion and facilitated diffusion. CHAPTER 7 GUIDED NOTES: MEMBRANE STRUCTURE AND FUNCTION 1. Explain the function of each and give an example Explain how facilitated diffusion works and give
CHAPTER 7 GUIDED NOTES: MEMBRANE STRUCTURE AND FUNCTION 1. Explain the function of each and give an example Explain how facilitated diffusion works and give Copy of Chapter 5 Pre-reading Questions Explain how facilitated diffusion works and give an example. Facilitated diffusion is the
21/06/2011В В· Facilitated diffusion is also called facilitated transport or passive mediated An example of this is Simple and facilitated diffusion are two types of 23/09/2013В В· Describe the process of diffusion and give an example. Explain the difference between simple diffusion and facilitated diffusion.
What Are Examples of Facilitated Diffusion? There are three main types of diffusion: simple, channel and facilitated Explain Facilitated Diffusion; Example of What Are Examples of Facilitated Diffusion? There are three main types of diffusion: simple, channel and facilitated Explain Facilitated Diffusion; Example of


